题目描述

对于非负整数 X 而言，X 的数组形式是每位数字按从左到右的顺序形成的数组。例如，如果 X = 1231，那么其数组形式为 [1,2,3,1]。

给定非负整数 X 的数组形式 A，返回整数 X+K 的数组形式。

示例 1：

输入：A = [1,2,0,0], K = 34
输出：[1,2,3,4]
解释：1200 + 34 = 1234

示例 2：

输入：A = [2,7,4], K = 181
输出：[4,5,5]
解释：274 + 181 = 455

示例 3：

输入：A = [2,1,5], K = 806
输出：[1,0,2,1]
解释：215 + 806 = 1021

示例 4：

输入：A = [9,9,9,9,9,9,9,9,9,9], K = 1
输出：[1,0,0,0,0,0,0,0,0,0,0]
解释：9999999999 + 1 = 10000000000

提示：

1 <= A.length <= 10000
0 <= A[i] <= 9
0 <= K <= 10000
If A.length > 1, then A[0] != 0

题目地址：https://leetcode.com/problems/add-to-array-form-of-integer/

题目大意

数组A表示了一个整数，K表示了一个整数，把两个数字相加，要求结果也是个数组形式的整数。

解题方法

前言

加法是我们上小学的时候开始学习的第一种数学运算。

在算法题中，「求加法」问题大多考察「列竖式」求和。

题目中，「两数之和」通常与其他形式表示的数字结合起来：

两个字符串形式的数字相加（第 415 题）
两个链表形式的数字相加（第 2 、445、369 题）
数组形式的数字相加（第 66 、989题）
两个二进制形式的数字相加（第 67 题）

做法都是非常类似的，本质是在考察各种数据表示形式：字符串，链表，数组，二进制。

我们只要掌握了用「列竖式」求「两数之和」的方法，这类题目全都可以秒杀。

十进制加法

我们先回顾一下十进制加法的计算过程：

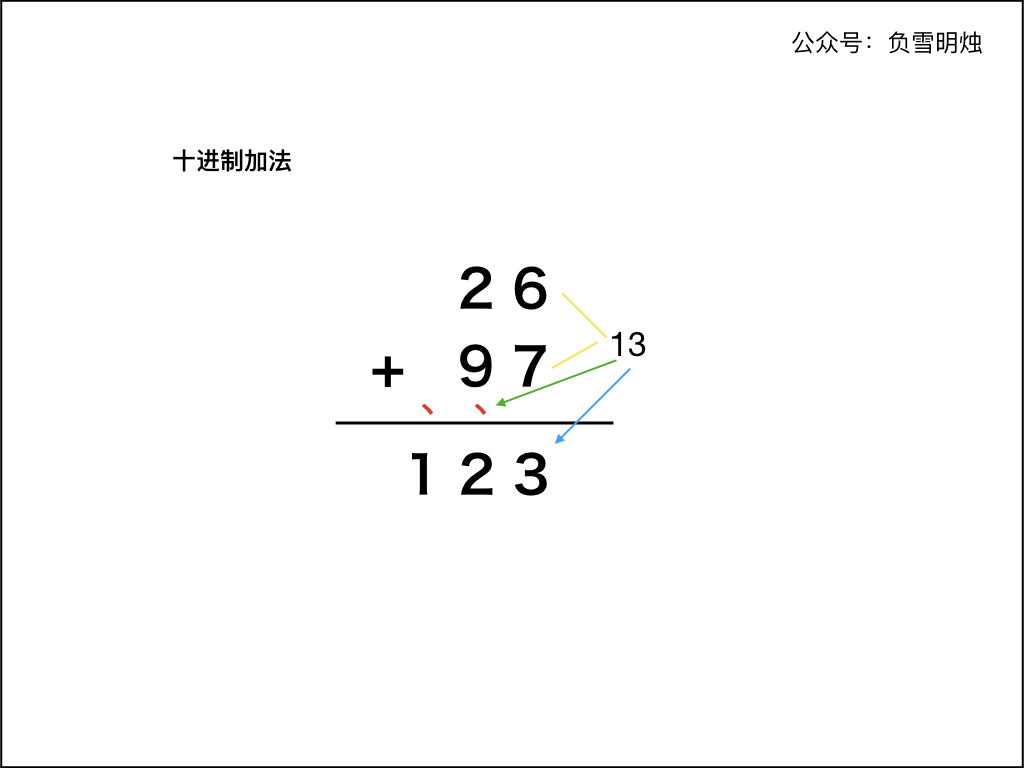
使用「竖式」计算十进制的加法的方式：

两个「加数」的右端对齐；
从最右侧开始，从右向左依次计算对应的两位数字的和，如果有进位需要加上进位。如果和大于等于 10，则把和的个位数字计入结果，并向前面进位；
重复步骤 2；
当两个「加数」的每个位置都计算完成，如果最后仍有进位，需要把进位数字保留到计算结果中。

在实现中需要注意的有：

不可以把字符串表示的「加数」先转化成 int 型数字再求和，因为可能溢出；
两个「加数」的字符串长度可能不同；
在最后，如果进位 carry 不为 0，那么最后需要计算进位。
注意结果数字是否为低位结果在前，根据题目要求判断最后是否要反转结果。

本题代码

题目要我们求一个数组形式表示的数字和一个 int 形式表示的数字相加，按照「列竖式」的方法进行求解即可。

代码说明

while (p1 >= 0 || k != 0 || carry > 0)含义：
1. 字符串 num 和数字 k 只要有一个没遍历完，那么就继续遍历；
2. 如果字符串 num 和数字 k 都遍历完了，但是最后留下的进位 carry != 0，那么需要把进位也保留到结果中。
取 adder 的时候，如果字符串 num 和数字 k 中有一个已经遍历完了（即 $p1 < 0$ 或者 $k = 0$），则认为 num 和 k 的对应位置是 $0$ 。

代码

该代码可以作为「求加法」的模板。

Java 代码如下：

class Solution {
    public List<Integer> addToArrayForm(int[] num, int k) {
        List<Integer> res = new ArrayList<>(); // 返回结果
        int p1 = num.length - 1; // 标记遍历到 num 的位置
        int carry = 0; // 进位
        while (p1 >= 0 || k != 0 || carry != 0) { // num 没遍历完，或 k 没遍历完，或进位不为 0
            int adder1 = p1 >= 0 ? num[p1] : 0; // 当前 num 的取值
            int adder2 = k % 10; // 当前 k 的位置，如果 k 已经是 0 那么 % 10 以后仍然是 0
            int sum = adder1 + adder2 + carry; // 当前位置相加的结果
            carry = sum >= 10 ? 1 : 0; // 是否有进位
            sum = sum >= 10 ? sum - 10 : sum; // 去除进位后留下的数字
            res.add(sum); // 把去除进位后留下的数字拼接到结果中
            p1 --; // 遍历到 num 的位置向左移动
            k /= 10; // 取 k 的下一个位置的数字
        }
        Collections.reverse(res); // 把结果反转
        return res; 
    }
}

C++ 代码如下：

class Solution {
public:
    string addStrings(string num1, string num2) {
        const int M = num1.size();
        const int N = num2.size();
        string res;
        int p1 = M - 1;
        int p2 = N - 1;
        int carry = 0;
        while (p1 >= 0 || p2 >= 0 || carry > 0) {
            int cur1 = p1 >= 0 ? num1[p1] - '0' : 0;
            int cur2 = p2 >= 0 ? num2[p2] - '0' : 0;
            int sum = cur1 + cur2 + carry;
            carry = sum >= 10 ? 1 : 0;
            sum = sum >= 10 ? sum - 10 : sum;
            res += to_string(sum);
            p1 --;
            p2 --;
        }
        reverse(res.begin(), res.end());
        return res;
    }
};

Python 代码如下：

class Solution(object):
    def addToArrayForm(self, num, k):
        p1 = len(num) - 1
        carry = 0
        res = []
        while p1 >= 0 or k != 0 or carry > 0:
            adder1 = num[p1] if p1 >= 0 else 0
            adder2 = k % 10
            sum = adder1 + adder2 + carry
            carry = 1 if sum >= 10 else 0
            sum = sum - 10 if sum >= 10 else sum
            res.append(sum)
            p1 -= 1
            k //= 10
        return res[::-1]